J.F. Owens, Florida State University
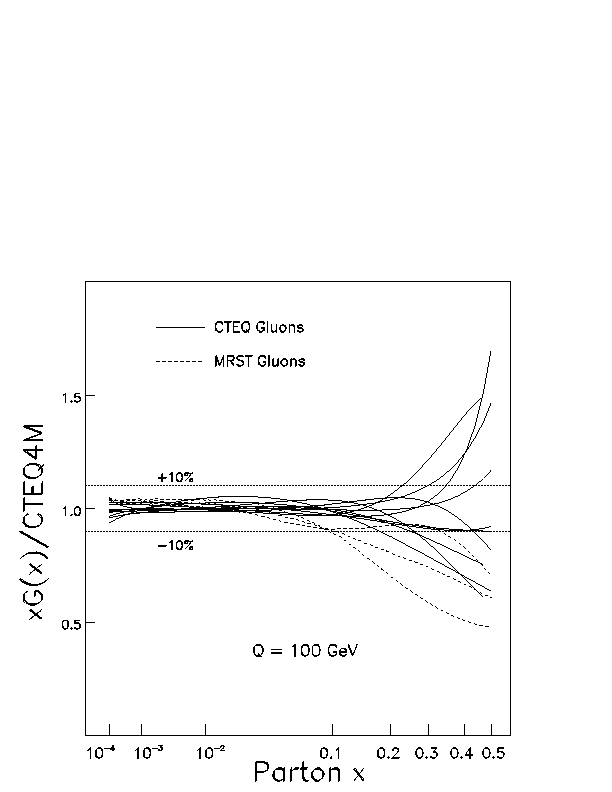
As the parton momentum fraction, x, tends towards one, all parton distributions beocme small, falling off as powers of (1-x). Thus, it has proven to be very difficult to satisfactorily determine the large-x behavior of the distributions. In the large-x region the sea quark terms have effectively vanished, leaving the valence quarks and the gluon distribution. Of these, the largest uncertainty is that of the gluon distribution as shown below. Also, see Huston et al., 1998. As x gets very near to one even the valence quark distributions have large uncertainties. While this may seem to be of academic interest only, this is far from the truth. The creation of massive new particles often is first observed in processes which use a significant amount of the overall center-of-mass energy and which, therefore, require x near 1. Thus, searches for new physical phenomena often rely on background estimates from conventional processes which invlolve the large-x region.
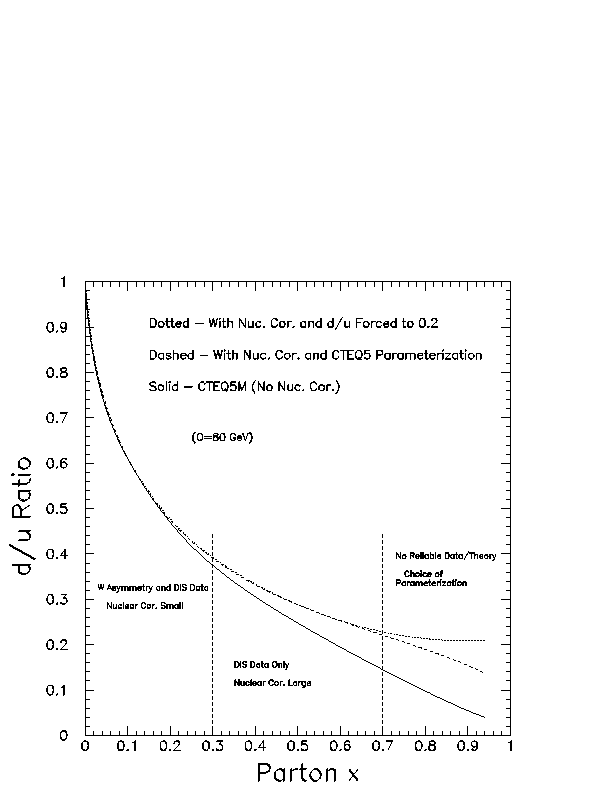
Recently, issues related to our knowledge of large-x parton distributions have been reexamined ( Kuhlmann et al., 2000). A significant portion of our knowledge of the d quark distribution comes from comparing deeply inelastic scattering on proton and deuterium targets. In the large-x region nuclear corrections can become important, which can therefore affect the extraction of neutron distributions from the deuterium data. Currently, our knowledge of the ratio of the d and u quarks as x goes to one is insufficient to say whether the ratio vanishes or goes to a finite constant at x equal to one (see the above reference for a summary and the figure below).
Another interesting feature is that the DGLAP evolution in Q^2 involves a "feed-down" mechanism. The parton distributions at particular values of of x and Q^2 depend on the values of the pdf's at higher x and lower Q^2. Therefore, the large-x, small Q^2 values feed down to lower values of x as Q^2 increases. Uncertainties in the large-x region can then propagate to lower values of x.
Commments on this entry may be sent to J.F. Owens.