MOMENTUM AND ENERGY OF ELEMENTARY PARTICLES

by
Dr. Stan Hirschi, Chair,
Phyiscs Dept. Central Michigan University

Goal: To use the momentum conservation law to analyze particle interactions as seen in bubble chamber pictures.

ACTIVITY ONE

MOMENTUM AND THE COLLISON OF ELEMENTARY PARTICLE

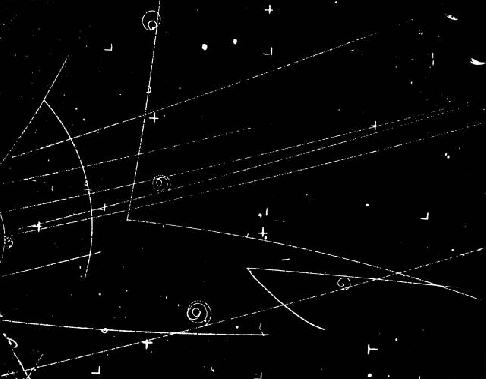
The concept of momentum and the Law of Momentum Conservation should be valid for microscopic objects as well as macroscopic objects. We should be able to apply these ideas to molecules (such as gas molecules), to atoms, and even to the elementary particles that are the constituents of atoms (electrons, protons, and neutrons). (The protons and neutrons of the atom are made up of yet smaller particles.) When they collide, they should behave just as billiard balls, cars, and footballs players do. How do we see collisions of these tiny particles? The answer to that is much like watching a jet plane fly high in the sky. Often, the plane will leave a vapor trail. The hot exhaust gases from combustion of the jet fuel will condense and allow us to see where the jet has been. With these small sub-atomic particles, the same can be made to happen. If a charged particle passes through a cloud (such as liquid hydrogen), the particles leave a "vapor" trail. The trail is actually small bubbles of hydrogen gas. Thus, we can see where the charged particle has been. Here’s an example of a hydrogen bubble chamber picture from the Lawrence Berkeley Lab archives:


[http://imglib.lbl.gov/ImgLib/COLLECTIONS/BERKELEY-LAB/PARTICLE- DETECTION/BUBBLE-CHAMBERS/images/96703039.lowres.jpeg]

Surely, the masses, momenta, and energies of these particles in standard metric units are all very small. (The mass of the proton is 1.67 X 10-27 kg!) This number, if used in any calculations, would constantly produce answers with similar powers of ten. Physicists often prefer to work with quantities that are not super small or super large. To simplify the data, we are going to express mass, momentum, and energy in units that are more comfortable to work with. In doing so, we will use a relationship that should be familiar to all, E = mc2, which of course is Einstein’s famous equation from relativity. If we now decide to measure energy in units of MeV, which is short for Million electron Volts, then we can generate the following list of units for momentum and mass:

Variable
SI Unit
Relativistic Unit
Momentum
Energy
Mass

We now have a convenient set of units for our particles with 1 MeV = 1.6 x 10-13 J.

Look closely at the hydrogen bubble chamber picture above. Make a list of observations about the tracks. Collisions are of projectile particles and protons (in liquid hydrogen).

You probably noticed that none of the lines is straight. (Get out your ruler!) All of the lines upon close examination are not straight but curved. If you could make the picture large enough, you would see that all of the lines are a part of circles (or spirals). This is because there is an external force acting on the charged particles which is always perpendicular to the direction of the particle’s motion. The condition for circular motion is:

Equation 1

 

The external force in this case is a magnetic force produced by a magnetic field that is placed around the bubble chamber. The magnetic force can be calculated by using the equation:

Equation 2

The variables are:

q, fundamental charge, usually ± 1e
v, velocity of the particle
B, magnetic field strength

Equating the magnetic force and the centripetal force we obtain:

Equation 3
Equation 4

For singly charged particles the equation can be reduced to:

Equation 5

where r is measured in centimeters, B in kilogauss, and p in MeV/c.

For the following questions, please refer to picture 2, below, which isolates a single collision from a bubble chamber photograph. The projectile is a negative pion (p -), while the target particle is, of course, a proton (p) at rest. Assume that the strength of the magnetic field B is equal to 30.0 kG (kilogauss) and is directed into the page. A length scale is also given.


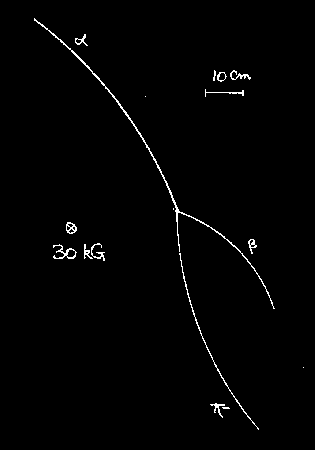
Picture 2 (In regular format)


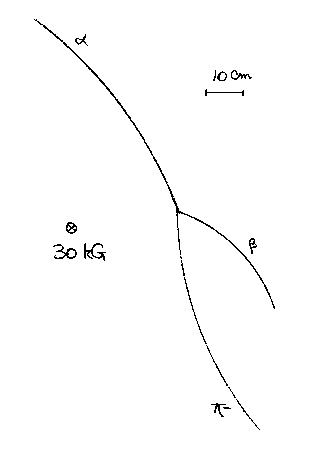
Picture 2 (In reversed format)

  1. In Picture 2, locate the collision.
  2. Using Picture 2, measure the radius r for the p -, a and b particles. (At this stage the identities of a and b are not known.) Before you do this, explain in detail how you will measure the radius. Your precision is very important to the accuracy of this activity.
  3. Construct a coordinate system (an x-y axis) at the vertex (center) of the collision. Using equation 5, determine the momentum (magnitude and direction) of each particle in units of MeV/c. Using appropriate methods, find the total momentum before the collision and, then, the total momentum after the collision. Is momentum conserved? Write a brief conclusion about your results of this activity.

ACTIVITY TWO

Goal: To use the conservation of energy to identify the mass of sub-atomic particles.

ENERGY AND THE COLLISION OF ELEMENTARY PARTICLES

The conservation of energy can be shown using the same data. However, since we are using sub-atomic particles that have a tremendous amount of kinetic energy (and a speed near the speed of light), the relationship between energy E and momentum p needs to be modified. To calculate the energy of particles, we use the relativistic momentum-energy equation:

Equation 6
Particle
Momentum (MeV/c)
p-
900
a
1089
b
387

  1. Using the table of momenta for the p -, a and b particles, compute the energies of each particle. (This is not a number but an expression.) Put the data in table form with the momentum and energy for each particle.

    Using the data, do some detective work.

  2. Is there evidence in the picture that tells you that we are indeed dealing with a collision between two particles and not a decay? (You probably will need to define collision and decay.)
  3. Identify the charge of a and b .

    Since we do not know the masses of the particles a and b , which is the case in most experiments, we need to make a guess at the masses and complete the calculations for the energies. If we select the correct masses, energy should be conserved and we will be relatively sure that those are the masses of the particles. Energy conservation requires:

    Equation 7

    The energy into an interaction must equal the energy out of the interaction.

  4. Using the table of sub-atomic particles and their masses, calculate the energies of a and b and put them in a data table. Using the conservation of energy, identify the mass of a and b . Remember you should first decide whether the collision is elastic or inelastic.
  5. Is it possible for this collision to produce a neutral particle?
  6. The particles a and b must be relatively stable since they exist for a time large enough to produce tracks in the photograph. From the age-old equation:

Equation 8

we can see that for particles moving near the speed of light, this equation becomes:

Equation 9

7. Using a metric ruler, what can you say about the lifetime of the particles?

ACTIVITY THREE

Goal: To use the conservation of energy and momentum to identify particles in elastic scattering, decay, and inelastic scattering.

Using the method above, continue the investigation of sub-atomic particles by analyzing the attached Pictures 3 and 4, as well as Picture 1, computing momenta and energies of the particles and identifying the particles, to whatever extent possible.

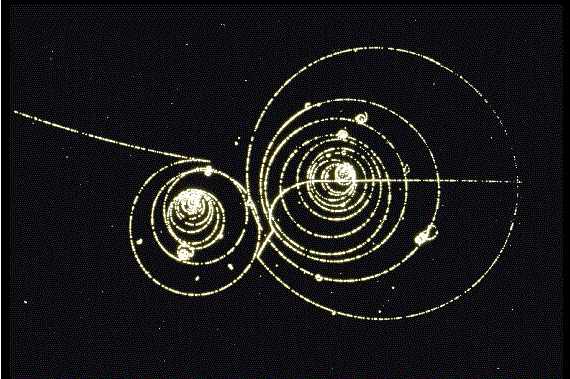
Picture 3
[http://wwwas.cern.ch/OpenDay/PressOffice/0310/009.jpeg]

Picture 4
[http://imglib.lbl.gov/ImgLib/COLLEC...HAMBERS/images/96703037.lowres.jpeg]

Questions? Comments??

James Gormley || Dr. Stan Hirschi