by
Dr. Stan Hirschi, Chair,
Phyiscs Dept. Central Michigan University
INTRODUCTION
Momentum and energy are basic concepts in physics. The Laws of Momentum and Energy Conservation make up the basis of our mechanical universe and are the backbone of Newtonian Mechanics. Much can be learned by studying the effects of macroscopic collisions and applying the Conservation Laws to these macroscopic interactions (such as two automobiles colliding). However, if students are to appreciate the full power of these Conservation Laws, then they need to see how these Laws are applied to areas of physics not normally included in the standard high school curriculum. The activities contained in this unit are intended to demonstrate this to the students with minimal extra learning (or teaching).
GENERAL INSTRUCTIONS: MOMENTUM
The student activity’s explanations are purposely devoid of much that is new. A case is made for the new units in which we measure the small quantities with which we will be dealing (similar to the atomic mass unit in Chemistry). Explain to students that like the metric prefixes used for large and small numbers, sometimes we need to change one of the measuring units when small or large quantities are used. If this made sense at all when they studied atomic mass units, it should make sense now, measuring small amounts of energy and momentum.
Since momentum and energy are usually taught after circular motion, the equations for circular motion should be familiar, but even if they are not, they can simply be stated as "this is what is used" and then be expanded upon when they are taught. This approach can also be used to introduce the magnetic force (Fm = qvB) and the momentum-energy equation E2 = (pc)2 + (mc2)2. If the idea is to introduce the students to such concepts and calculation, the simple use of given equations should suffice. The conservation laws will be shown to be valid for these microscopic elastic collisions reinforcing the fact that regardless of the size of the particles involved in elastic collisions, momentum and energy are always conserved. Using the conservation laws to predict the identity of particles will be the final activity demonstrating the usefulness of these conservation laws.
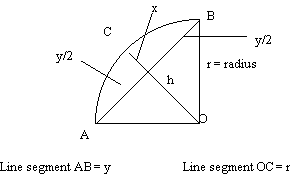
For questions one and two, discussion can be used to help the students identify the curved lines and the collision or decay. A brief review at this point of elastic and in-elastic collisions is advised. For question three, students should be given "free range" to attempt measuring the radius of curvature. However, an alternative method follows.
Diagram 1
From the diagram, it can be shown that:
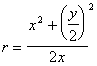Equation 1
which will give the radius of the curve. The derivation of this equation will be left to the discretion of the teacher. This derivation may be an excellent source of extra credit for the students.
Construction of the line segment y and line segment x as the perpendicular bisector of y is a geometric task that the students can easily accomplish. Though this is possibly the most direct measurement of the radius r, students should be encouraged to use their imaginations about possible solutions. It is recommended, however, that they defend their choice of measurement method including its precision and accuracy. The accuracy of this experiment is directly proportional to the precision of their measurements. This fact will need to be reinforced by the teacher. Physicists must be concerned about precision and accuracy on a daily basis. This fact must be conveyed to the students. This might possibly be accomplished by asking them to estimate the error based upon their measurement precision.
The students may need a little help constructing the coordinate axis system so the relative direction of the velocity of the particles can be obtained. Although this technique may have been taught at the beginning of the study of vectors, a review may be necessary. Once the momentum has been established, that is magnitude and direction, then conventional methods can be used to show conservation. A vector diagram drawn to scale is one option but very lengthy. Mathematical methods include using vector components or using triangles and the law of sines and the law of cosines.
GENERAL INSTRUCTIONS: ENERGY
Two of the names for the particles have been arbitrarily chosen as a and b ; the particle p is actually the pion particle. Students should be encouraged to guess at solutions for the masses of the particles. The conservation laws must be valid and therefore only the correct mass will produce conservation of energy. Explain to them that a small percentage error is to be expected since the measurements made in the previous activity have error and all calculations rely on these measurements. This is what actually happens when such Bubble Chamber pictures are evaluated. As a whole, this is a real lesson on how science, especially real physics, works.
In the final activity, the students are encouraged to do extra calculations on another Bubble Chamber picture. The time component will be the determining factor whether this lesson is used. Many sites on the Internet provide readable sources as well as pictures for study. The attached bibliography includes a list of some sites. However, do not be surprised if your students find additional locations. They are very capable at searching the web.
WEB SITES
http://publish.aps.org????Physics Review Focus
http://www.aip.org/physnews???American Institute of Physics
http://www.fnal.gov/pub/standardmodel.html?Fermilab
http://www.hep.net/educational/edu.html??HEP Educational Links
http://el.www.media.mit.edu/groups??StarLogo Bubble Chamber Project
NOTE:
For all its possibilities, the web is a bit transitory. Too often it is ‘here today, gone tomorrow.’
Questions? Comments??
James Gormley