|
PHY 4822
|
Elementary Particles
in a Bubble Chamber
|
Introduction
Elementary particles are everywhere around us. Apart from the standard
matter particles proton, neutron and electron, hundreds of other particles
have been found, produced in cosmic ray interactions in the atmosphere
or by accelerators. Hundreds of charged particles traverse our bodies per
second, and some will damage our DNA, one of the reasons for the existence
of a sophisticated DNA repair mechanism in the cell.
The data for this experiment is in the form of a bubble chamber
photograph which shows bubble tracks made by elementary particles as they
traverse liquid hydrogen. In the experiment under study, a beam of low-energy
negative pions (p- beam) hits a hydrogen
(p for proton) target inside the bubble chamber. The bubble
chamber is essentially a container with liquid hydrogen normally kept just
below its boiling point (T=20 K). As the pions enter the detector
a piston slightly decompresses the liquid so it becomes ``super-critical''
and starts boiling, and
bubbles form, first at the ionization trails left by the charged
particles traversing the liquid.
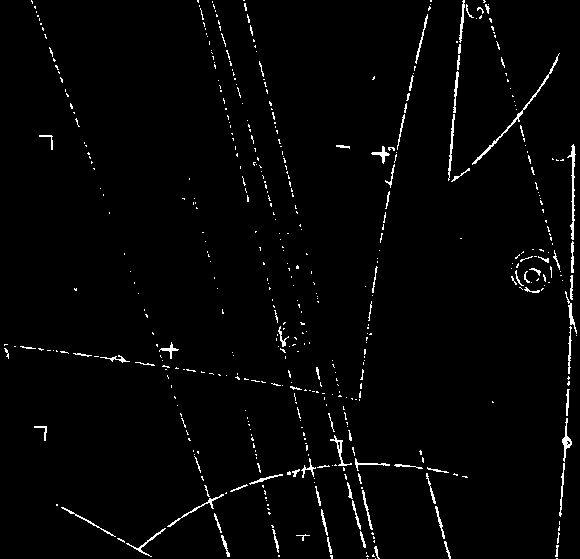
Figure 1: Photograph of the interaction between a high-energy p--meson
from the Berkeley Bevatron accelerator and a proton in a liquid hydrogen
bubble chamber, which produces two neutral particles L0
and K0, which are short-lived and decay into charged
particles a bit further. |
|
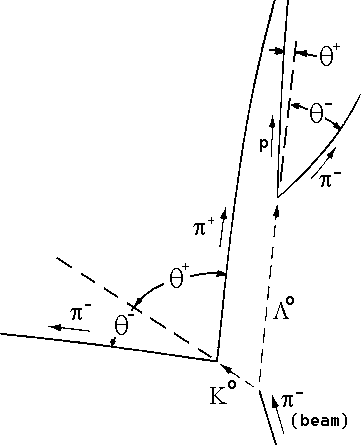
Figure 2: Illustration of the interaction, and identification of bubble
trails and variables
to be measured in the photograph in Figure
3.
The reaction shown in Figure 1 shows the production of a pair of neutral
particles (that do not leave a ionized trail in their wake),
which after a short while decay into pairs of charged particles:
p- + p ®L0
+ K0 ,
where the neutrals decay as follows:
L0 ®
p
+ p- ,
K0 ® p+
+ p- .
In this experiment, we assume the masses of the proton (mp
= 938.3 MeV/c2) and the pions (mp
+
= mp- = 139.4 MeV/c2)
to be known precisely, and we shall determine the masses of the
L0
and the K0, also in these mass energy units.
Momentum measurement
In order to "reconstruct'' the interaction completely, one uses the conservation
laws of (relativistic) momentum and energy, plus the knowledge of the initial
pion beam parameters (mass and momentum). In order to measure momenta of
the produced charged particles, the bubble chamber is located inside a
magnet that bends the charged particles in helical paths. The 1.5 T magnetic
field is directed up out of the photograph. The momentum p of each
particle is directly proportional to the radius of curvature r,
which in turn can be calculated from a measurement of the "chord length''
and "sagitta" s as:
r = [l2/(8s)] + [s/2] .
Note, that the above is strictly true only if all momenta are perfectly
in the plane of the photograph; in actual experiments stereo photographs
of the interaction are taken to be able to reconstruct the interaction
in all three dimensions. The interaction in this photograph was specially
selected for its planarity.
In the reproduced photograph the actual radius of curvature R
of the track in the bubble chamber is multiplied by the magnification factor
m,
r
= mR. For the reproduction in Figure 3
m = height of photograph
(in mm) divided by 173 mm.
The momentum p of the particles is proportional to their radius
of curvature R in the chamber. To derive this relationship for
relativistic
particles we begin with Newton's law in the form:
F = dp/dt =
e v×B
(Lorentz force).
Here the momentum (p) is the relativistic momentum mvg,
where the relativistic g-factor is defined in
the usual way
g = [Ö(1-v2/c
2)]-1.
Thus, because the speed v is constant:
F = dp/dt = d(mv
g)/dt
= mg dv/dt = m
g
(v2/R)(-r) = e v B (-r
)
,
where r is the unit vector in the radial direction.
Division by v on both sides of the last equality finally yields:
mgv / R = p
/ R = e B ,
identical to the non-relativistic result! In atomic units we find:
| p c (in eV) = c R B ,
thus p (in MeV/c) = 2.998×108R
B ×10-6 = 300 R(in m) B(in T) |
(1) |
Measurement of angles
Draw straight lines from the point of primary interaction to the points
where the L0 and the K0
decay. Extend the lines beyond the decay vertices. Draw tangents to the
four decay product tracks at the two vertices. (Take care drawing these
tangents, as doing it carelessly is a source of large errors.)
Use a protractor
to measure the angles of the decay product tracks relative to the parent
directions (use Fig. 3 for measurements and Fig. 2 for definitions).
Analysis
The laws of relativistic kinematics relevant to this calculation are written
below. We use the subscripts zero, plus, and minus to refer to the charges
of the decaying particles and the decay products.
| p+sinq+
= p-sinq- |
(2) |
| p0 = p+cosq+
+ p-cosq- |
(3) |
E0 = E+ +
E-,
where E+ =
Ö(p+
2c2
+ m+2c4) ,
and E- = Ö
(p-2c2
+ m-2c4) |
|
| m0c2 = Ö(E02
- p02c2) |
|
Note that there is a redundancy here. That is, if p+,
p-,
q+,
and q- are all known, equation (2)
is not needed to find m0. In our two-dimensional case
we have two equations (2 and 3), and only one unknown quantity
m0,
and the system is over-determined. This is fortunate, because sometimes
(as here) one of the four measured quantities will have a large experimental
error. When this is the case, it is usually advantageous to use only three
of the variables and to use equation (2) to calculate the fourth.
Alternatively, one may use the over-determination to "fit'' the m0,
and to determine it more precisely.
K0 decay.
-
Measure three of the quantities r+, r-,
q+, and q-.
Omit the one which you believe would introduce the largest experimental
error if used to determine mK.
-
Use the magnification factor m to calculate the actual radii R
and equation (1) to calculate the momenta
(in MeV/c) of one or both pions.
-
Use the equations above to determine the rest mass (in MeV/c2)
of the K0.
-
Carefully estimate the error in your result from the errors in the measured
quantities.
L0 decay:
-
The proton track is too straight to be well measured in curvature. Also,
q+
is small, and the value of mL
is quite sensitive to this measurement. Assume that q+
= (0.32±0.05)° (check
this with your protractor). Measure r- and q-.
-
Calculate mL and its error
the same way as for the K0.
-
Finally, compare your values with the accepted mass values (the world average),
and discuss.
Bonus question:
(25% extra credit)
Calculate the momenta for both neutral particles, and hence find their
lifetimes, both in the laboratory, and in their own rest-frames. Compare
the latter with the accepted values [3].
References:
[1] G.D. Coughlan and J.E. Dodd: “The ideas of particle
physics”,
Cambridge Univ. Press, Cambridge
1991
[2] “The Particle Adventure”, http:// pdg.lbl.gov/cpep/adventure.html
[3] Review of Particle Physics, by the Particle Data Group,
European
Physical Journal C3 (1998) 1 - 794
(previous edition: Physical
Review
D54 (1996) 1 - 720) (available on WWW: http://pdg.lbl.gov)
[4] Kenneth Krane: Modern Physics, 2nd ed. ; John Wiley &
Sons, New York 1996
Figure 3 (Next Page): Photograph of the interaction between a
high-energy p--meson from the Berkeley
Bevatron accelerator and a proton in a liquid hydrogen bubble chamber.
The interaction produces two neutral particles L0
and K0, which are short-lived and decay into charged
particles. The photo covers an area (H•W) of 173 mm • 138 mm of the bubble
chamber. In this enlargement the magnification factor g = (height
(in mm) of the photograph)/(173 mm).

Note: Experiment adapted from PHY 251 lab at SUNY at Stony Brook (Michael
Rijssenbeek) of


