The animation linked below was developed by Michael Eichberg during his internship at FSU's Supercomputer Computation Research Institute. It relies on simulations performed on an

The initial simulation is performed with

i.e. completely disordered. Updates of the b(E) function are displayed after 100 iterations of 1000 sweeps each. A single iteration of b(E) relies on the energy histogram from 1000 sweeps sampled since the previous iteration. The summed up histograms for 100 iterations are displayed as H(E). The following picture is the first one of the animation.

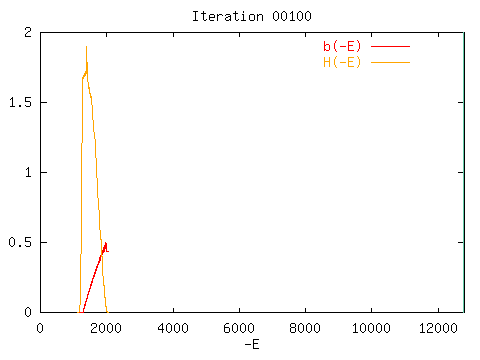
Note that the negative energy -E is used on the abscissa and the vertical line to the right of the figure is at the minimum energy, E = -12776, targetted in the simulation (the absolute minimum of the system is at E = -12800). Once the targetted minimum energy is reached, the line will move to E = -1280, which is the average energy for the system at infinite temperature, i.e. beta=0. It will move back to E = -12776 when E = -1280 is hit (what happens then quickly) and so on. The fugacities a(E) follow from b(E) and are not displayed. To view the animation applets have to be enabled on your browser.

In the animation above a constant extrapolation of b(E), indicated by a tiny extension of the b(E) function, has been used at small energies (-E large) which have not yet been visited, see cond-mat/9909236 for more details. However, the performace without such an extrapolation is almost unchanged. Just the the "pioneering" edge of the b(E) function is much noisier as our next animation shows: