|
Introduction
The multicanonical (MUCA) Monte Carlo (MC) method
calculates expectation values of the Gibbs ensemble for a
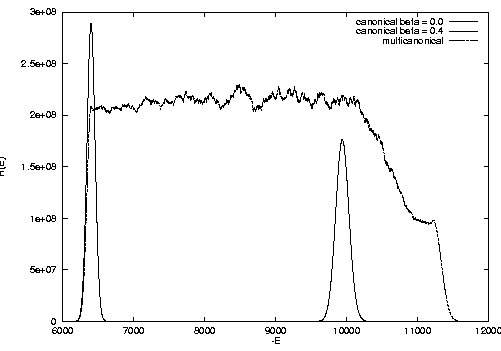
desired temperature range. The subsequent figure depicts
histograms from Gibbs canonical and multicanonical MC
simulations of the 2d Ising model on an 80x80
lattice at temperature
T=1/beta.
The canonical simulations were carried out at
beta=0
and
beta=0.4.
The multicanonical simulation covered the range
beta=0 to
beta=0.449.
 Conventional, canonical MC simulations sample with the Boltzmann weight
exp [ - beta E ]
where E
is the energy of the system. MUCA simulations sample with a
weight function
exp [ - b(E) E + a(E) ]
which needs to be determined recursively. The
fugacity a(E)
follows from b(E)
which is related to the
microcanonical temperature T(E)
by
b(E) = 1 / T(E)
and the simulated MUCA temperature range is, essentially,
determined by the extrema of T(E). A
recursive estimate of b(E)
is therefore necessary before the proper MUCA simulation can
begin. With respect to this progress has been made in
recent years. The following link
Multicanonical RecursionBack to MUCA homepage |